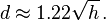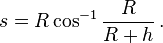What is it?

Horizonal.js takes any static HTML document and transforms it into a collection of discrete "pages". The transitions between one page an the next can then be programmed via CSS transforms, CSS animations, JavaScript, or any combination of these.

Disable Horizonal with the switch above and you'll see that this is just a regular old HTML document. Try out some of the themes to get a taste of the kind of effects that can be achieved.

What's It For?

Horizonal.js grew out of some simple experimentation with CSS transforms and animations, and if nothing else it is a showcase for the cool visual effects that can be achieved through these technologies.

Other use cases could be slides for presentations, image galleries, portfolios, marketing websites, or whatever else you can think of. Note that this is very much an experimental project, so be careful and test well before using in production!

Features

• Fully customizable - limited only by your imagination (and JavaScript & CSS chops)
• Touch-enabled: page through the document by swiping.
• Keyboard control with arrow keys.
• Can handle URL fragments - e.g. go to that poem
• Can handle large elements that span multiple pages - e.g. this huge photo
• Rich API allowing programmatic control of paging.
• Faithfully reproduces even complex layouts using grid systems.

Performance

The demos on this page make use of some pretty new features of CSS, and as a result, browser support can be inconsistent at times, but all should work well on the latest browser versions.

Also to note is that the initial calculation of the page layouts is fairly processor-intensive, so on mobile devices in particular, a little delay in loading is to be expected. Depending on the complexity of the transition effect, your device may exhibit a little choppiness if it does not have the power to keep up.

Try It Out

If you know some CSS and JavaScript, try out the interactive playground on Plunker:

The Horizon

The horizon (or skyline) is the apparent line that separates earth from sky, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting intersection of earth and sky is called the visible horizon. When looking at a sea from a shore, the part of the sea closest to the horizon is called the offing. The word horizon derives from the Greek "ὁρίζων κύκλος" horizōn kyklos, "separating circle", from the verb ὁρίζω horizō, "to divide", "to separate", and that from "ὅρος" (oros), "boundary, landmark".

Appearance and usage

Historically, the distance to the visible horizon at sea has been extremely important as it represented the maximum range of communication and vision before the development of the radio and the telegraph. Even today, when flying an aircraft under Visual Flight Rules, a technique called attitude flying is used to control the aircraft, where the pilot uses the visual relationship between the aircraft's nose and the horizon to control the aircraft. A pilot can also retain his or her spatial orientation by referring to the horizon.

In many contexts, especially perspective drawing, the curvature of the Earth is disregarded and the horizon is considered the theoretical line to which points on any horizontal plane converge (when projected onto the picture plane) as their distance from the observer increases. For observers near sea level the difference between this geometrical horizon (which assumes a perfectly flat, infinite ground plane) and the true horizon (which assumes a spherical Earth surface) is imperceptible to the naked eye (but for someone on a 1000-meter hill looking out to sea the true horizon will be about a degree below a horizontal line).

In astronomy the horizon is the horizontal plane through (the eyes of) the observer. It is the fundamental plane of the horizontal coordinate system, the locus of points that have an altitude of zero degrees. While similar in ways to the geometrical horizon, in this context a horizon may be considered to be a plane in space, rather than a line on a picture plane.

Distance to the horizon

Ignoring the effect of atmospheric refraction, distance to the horizon from an observer close to the Earth's surface is about

where d is in kilometres and h is height above ground level in metres.

Examples:

• For an observer standing on the ground with h = 1.70 metres (5 ft 7 in) (average eye-level height), the horizon is at a distance of 4.7 kilometres (2.9 mi).
• For an observer standing on the ground with h = 2 metres (6 ft 7 in), the horizon is at a distance of 5 kilometres (3.1 mi).
• For an observer standing on a hill or tower of 100 metres (330 ft) in height, the horizon is at a distance of 36 kilometres (22 mi).
• For an observer standing at the top of the Burj Khalifa (828 metres (2,717 ft) in height), the horizon is at a distance of 103 kilometres (64 mi).
• For an observer atop Mount Everest (8,848 metres (29,029 ft) altitude), the horizon is at a distance of 336 kilometres (209 mi).

With d in miles and h in feet,

Examples, assuming no refraction:

• For an observer on the ground with eye level at h = 5 ft 7 in (1.70 m), the horizon is at a distance of 2.9 miles (4.7 km).
• For an observer standing on a hill or tower 100 feet (30 m) in height, the horizon is at a distance of 12.2 miles (19.6 km).
• For an observer on the summit of Aconcagua (22,841 feet (6,962 m) in height), the sea-level horizon to the west is at a distance of 184 miles (296 km).
• For U-2 pilot, whilst flying at its service ceiling 70,000 feet (21,000 m), the horizon is at a distance of 324 miles (521 km)

Geometrical model

If the Earth is assumed to be a sphere with no atmosphere then the distance to the horizon can easily be calculated. (The Earth's radius of curvature actually varies by 1% between the Equator and the Poles, so this formula isn't absolutely exact even assuming no refraction.)

The secant-tangent theorem states that

Make the following substitutions:

• d = OC = distance to the horizon
• D = AB = diameter of the Earth
• h = OB = height of the observer above sea level
• D+h = OA = diameter of the Earth plus height of the observer above sea level

The formula now becomes

or

where R is the radius of the Earth.

The equation can also be derived using the Pythagorean theorem. Since the line of sight is a tangent to the Earth, it is perpendicular to the radius at the horizon. This sets up a right triangle, with the sum of the radius and the height as the hypotenuse. With

• d = distance to the horizon
• h = height of the observer above sea level
• R = radius of the Earth

referring to the second figure at the right leads to the following:

Another relationship involves the distance s along the curved surface of the Earth to the horizon; with γ in radians,

then

Solving for s gives

The distance s can also be expressed in terms of the line-of-sight distance d; from the second figure at the right,

substituting for γ and rearranging gives

The distances d and s are nearly the same when the height of the object is negligible compared to the radius (that is, h ≪ R).

Multi-page spanning

For an observer standing at the top of the Burj Khalifa (828 metres (2,717 ft) in height), the horizon is at a distance of 103 kilometres (64 mi).